(問題)
確率変数 \( X\) と \( Y\) が独立であるとき
確率変数 \( X\) と \( Y\) が独立であるとき
\begin{align*}
&(1)~E(X+Y)=E(X)+E(Y)\\\\
&(2)~V(X+Y)=V(X)+V(Y)\\\\
&(3)~V(X-Y)=V(X)+V(Y)\\\\
&(4)~V(aX)=a^{2}V(X)\\\\
\end{align*}
&(1)~E(X+Y)=E(X)+E(Y)\\\\
&(2)~V(X+Y)=V(X)+V(Y)\\\\
&(3)~V(X-Y)=V(X)+V(Y)\\\\
&(4)~V(aX)=a^{2}V(X)\\\\
\end{align*}
が成り立つことを証明せよ。
復習
確率変数 \( X\) の平均値(期待値) \( E(X)\) および分散 \( V(X)\) の定義は
\begin{align*}
E(X)&=\displaystyle \sum_{i}i\cdot P(X=i)\\\\
V(X)&=\displaystyle \sum_{i}(i-E(X))^{2}\cdot P(X=i)\\\\
&=E(X^2)-(E(X))^2.
\end{align*}
E(X)&=\displaystyle \sum_{i}i\cdot P(X=i)\\\\
V(X)&=\displaystyle \sum_{i}(i-E(X))^{2}\cdot P(X=i)\\\\
&=E(X^2)-(E(X))^2.
\end{align*}
例えば、\( 1\) から \( 6\) までの数字を書いたサイコロを投げたときに、出た目の数の平均値 \( E(X)\) は
\begin{align*}
E(X)&=\displaystyle \sum_{i}^{6}i\cdot P(X=i)=\displaystyle \sum_{i}\cdot \frac{1}{6}=\frac{7}{2}.
\end{align*}
E(X)&=\displaystyle \sum_{i}^{6}i\cdot P(X=i)=\displaystyle \sum_{i}\cdot \frac{1}{6}=\frac{7}{2}.
\end{align*}
分散 \( V(X)\) は
\begin{align*}
V(X)&=\displaystyle \sum_{i}^{6}\left(i-\frac{7}{2}\right)^{2}P(X=i)\\
&=\displaystyle \sum_{i}^{6}\left(i-\frac{7}{2}\right)^{2}\cdot \frac{1}{6}\\
&=2\cdot\left(\frac{5}{2}\right)^{2}+2\cdot\left(\frac{3}{2}\right)^{2}+2\cdot \left(\frac{1}{2}\right)^{2}\\
&=\frac{35}{12}
\end{align*}
V(X)&=\displaystyle \sum_{i}^{6}\left(i-\frac{7}{2}\right)^{2}P(X=i)\\
&=\displaystyle \sum_{i}^{6}\left(i-\frac{7}{2}\right)^{2}\cdot \frac{1}{6}\\
&=2\cdot\left(\frac{5}{2}\right)^{2}+2\cdot\left(\frac{3}{2}\right)^{2}+2\cdot \left(\frac{1}{2}\right)^{2}\\
&=\frac{35}{12}
\end{align*}
または、分散は次のようにも求めることができる。
\begin{align*}
V(X)&=E(X^{2})-(E(X))^{2}\\
&=\displaystyle \sum_{i}^{6}i^{2}\cdot P(X=i)-\left(\frac{7}{2}\right)^{2}\\
&=\frac{1}{6}\displaystyle \sum_{i}^{6}i^{2}-\left(\frac{7}{2}\right)^{2}\\
&=\frac{1}{6}\frac{6(6+1)(2\cdot 6 +1)}{6}-\left(\frac{7}{2}\right)^{2}\\
&=\frac{35}{12}
\end{align*}
V(X)&=E(X^{2})-(E(X))^{2}\\
&=\displaystyle \sum_{i}^{6}i^{2}\cdot P(X=i)-\left(\frac{7}{2}\right)^{2}\\
&=\frac{1}{6}\displaystyle \sum_{i}^{6}i^{2}-\left(\frac{7}{2}\right)^{2}\\
&=\frac{1}{6}\frac{6(6+1)(2\cdot 6 +1)}{6}-\left(\frac{7}{2}\right)^{2}\\
&=\frac{35}{12}
\end{align*}
場合に応じて使い分けましょう。
(1) \( E(X+Y)=E(X)+E(Y)\) の証明
確率変数 \( X\) と \( Y\) が独立である、すなわち、
\begin{align*}
P((X,Y)=(i,j))=P(X=i)\cdot P(Y=j)
\end{align*}
P((X,Y)=(i,j))=P(X=i)\cdot P(Y=j)
\end{align*}
であるとき、
\begin{align*}
E(X+Y)&=\displaystyle \sum_{i,j}(i+j)P((X,Y)=(i,j))\\
&=\displaystyle \sum_{i,j}(i+j))P(X=i)P(Y=j)\\
&=\displaystyle \sum_{i,j}i\cdot P(X=i)P(Y=j)+\displaystyle \sum_{i,j}j\cdot P(X=i)P(Y=j)\\
&=\displaystyle \sum_{j}[\displaystyle \sum_{i}\cdot P(X=i)]P(Y=j)+\displaystyle \sum_{i}[\displaystyle \sum_{j}\cdot P(X=j)]P(X=i)\\
&=E(X)\displaystyle \sum_{j}P(Y=j)+E(Y)\displaystyle \sum_{i}P(X=i)\\
&=E(X)+E(Y).
\end{align*}
E(X+Y)&=\displaystyle \sum_{i,j}(i+j)P((X,Y)=(i,j))\\
&=\displaystyle \sum_{i,j}(i+j))P(X=i)P(Y=j)\\
&=\displaystyle \sum_{i,j}i\cdot P(X=i)P(Y=j)+\displaystyle \sum_{i,j}j\cdot P(X=i)P(Y=j)\\
&=\displaystyle \sum_{j}[\displaystyle \sum_{i}\cdot P(X=i)]P(Y=j)+\displaystyle \sum_{i}[\displaystyle \sum_{j}\cdot P(X=j)]P(X=i)\\
&=E(X)\displaystyle \sum_{j}P(Y=j)+E(Y)\displaystyle \sum_{i}P(X=i)\\
&=E(X)+E(Y).
\end{align*}
(2) \( V(X+Y)=V(X)+V(Y)\) の証明
\begin{align*}
V(X+Y)&=E((X+Y)^{2})-(E(X+Y))^{2}\\
&=E(X^{2}+2XY+Y^{2})-(E(X)+E(Y))^{2}\\
&=E(X^{2})+2E(XY)+E(Y^{2})-(E(X))^{2}-2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})+2E(X)E(Y)+E(Y^{2})-(E(X))^{2}-2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})-(E(X))^{2}+E(Y^{2})-(E(Y))^{2}\\
&=V(X)+V(Y)
\end{align*}
V(X+Y)&=E((X+Y)^{2})-(E(X+Y))^{2}\\
&=E(X^{2}+2XY+Y^{2})-(E(X)+E(Y))^{2}\\
&=E(X^{2})+2E(XY)+E(Y^{2})-(E(X))^{2}-2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})+2E(X)E(Y)+E(Y^{2})-(E(X))^{2}-2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})-(E(X))^{2}+E(Y^{2})-(E(Y))^{2}\\
&=V(X)+V(Y)
\end{align*}
(3) \( V(X-Y)=V(X)+V(Y)\) の証明
\begin{align*}
V(X-Y)&=E((X-Y)^{2})-(E(X-Y))^{2}\\
&=E(X^{2}-2XY+Y^{2})-(E(X)-E(Y))^{2}\\
&=E(X^{2})-2E(XY)+E(Y^{2})-(E(X))^{2}+2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})-2E(X)E(Y)+E(Y^{2})-(E(X))^{2}+2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})-(E(X))^{2}+E(Y^{2})-(E(Y))^{2}\\
&=V(X)+V(Y)
\end{align*}
V(X-Y)&=E((X-Y)^{2})-(E(X-Y))^{2}\\
&=E(X^{2}-2XY+Y^{2})-(E(X)-E(Y))^{2}\\
&=E(X^{2})-2E(XY)+E(Y^{2})-(E(X))^{2}+2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})-2E(X)E(Y)+E(Y^{2})-(E(X))^{2}+2E(X)E(Y)-(E(Y))^{2}\\
&=E(X^{2})-(E(X))^{2}+E(Y^{2})-(E(Y))^{2}\\
&=V(X)+V(Y)
\end{align*}
(4) \( V(aX)=a^{2}V(X)\) の証明
\begin{align*}
V(aX)&=E((aX)^{2})-(E(aX))^{2}\\
&=E(a^{2}X^{2})-(E(aX))^{2}\\
&=a^{2}E(X^{2})-(aE(X))^{2}\\
&=a^{2}E(X^{2})-a^{2}(E(X))^{2}\\
&=a^{2}(E(X^{2})-(E(X))^{2})\\
&=a^{2}V(X).
\end{align*}
V(aX)&=E((aX)^{2})-(E(aX))^{2}\\
&=E(a^{2}X^{2})-(E(aX))^{2}\\
&=a^{2}E(X^{2})-(aE(X))^{2}\\
&=a^{2}E(X^{2})-a^{2}(E(X))^{2}\\
&=a^{2}(E(X^{2})-(E(X))^{2})\\
&=a^{2}V(X).
\end{align*}

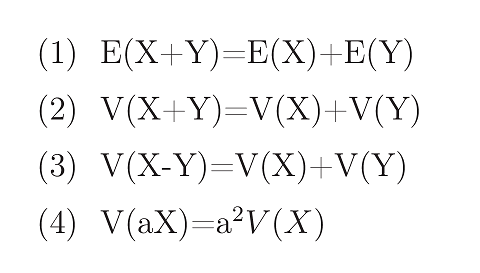

コメント