(問題1)
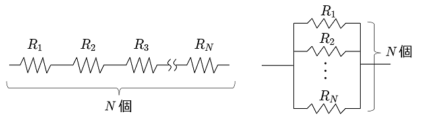
それぞれ独立な \(N\) 個の抵抗を直列に繋いだ合成抵抗の平均値と標準偏差を求めよ.ただし、各抵抗は \( N(R,\sigma ^{2})\) の正規分布に従うものとする.
それぞれ独立な \(N\) 個の抵抗を直列に繋いだ合成抵抗の平均値と標準偏差を求めよ.ただし、各抵抗は \( N(R,\sigma ^{2})\) の正規分布に従うものとする.
それぞれの抵抗は独立であるから,
\begin{align*}
E(R_{1}+R_{2}+\cdots+R_{N})=E(R_{1})+E(R_{2})+\cdots+E(R_{N})=NR\\\\
V(R_{1}+R_{2}+\cdots+R_{N})=V(R_{1})+V(R_{2})+\cdots+V(R_{N})=N\sigma ^{2}.
\end{align*}
E(R_{1}+R_{2}+\cdots+R_{N})=E(R_{1})+E(R_{2})+\cdots+E(R_{N})=NR\\\\
V(R_{1}+R_{2}+\cdots+R_{N})=V(R_{1})+V(R_{2})+\cdots+V(R_{N})=N\sigma ^{2}.
\end{align*}
したがって, \(N\) 個の抵抗を直列に繋いだ合成抵抗の平均値は \( NR\) ,標準偏差は \( \sqrt{N}\sigma\)
(問題2)
それぞれ独立な \(N\) 個の抵抗を並列に繋いだ合成抵抗の平均値と標準偏差を求めよ.ただし,各抵抗は \( N(R,\sigma ^{2})\) の正規分布に従うものとする.
それぞれ独立な \(N\) 個の抵抗を並列に繋いだ合成抵抗の平均値と標準偏差を求めよ.ただし,各抵抗は \( N(R,\sigma ^{2})\) の正規分布に従うものとする.
\( i\) 番目における抵抗を \( R_{i}\) と表し,平均値からのずれ(誤差)を \(\varepsilon_{i}\) とすると、$$R_{i}=R+\varepsilon_{i}$$と表せる。\( \frac{1}{R_{i}}=\frac{1}{R+\varepsilon_{i}}\) の近似式を考えると、
\begin{align*}
\frac{1}{R_{i}}=\frac{1}{R+\varepsilon_{i}}&=\frac{1}{R}\frac{1}{1+\frac{\varepsilon_{i}}{R}}\\\\
&=\frac{1}{R}\left(1-\frac{\varepsilon_{i}}{R} + \left(\frac{\varepsilon_{i}}{R} \right)^{2}-\left(\frac{\varepsilon_{i}}{R} \right)^{3}+\cdots\right)\\\\
&\approx \frac{1}{R}-\frac{\varepsilon_{i}}{R^{2}}\\\\
&=\dfrac{R-\varepsilon_{i}}{R^{2}}
\end{align*}
\frac{1}{R_{i}}=\frac{1}{R+\varepsilon_{i}}&=\frac{1}{R}\frac{1}{1+\frac{\varepsilon_{i}}{R}}\\\\
&=\frac{1}{R}\left(1-\frac{\varepsilon_{i}}{R} + \left(\frac{\varepsilon_{i}}{R} \right)^{2}-\left(\frac{\varepsilon_{i}}{R} \right)^{3}+\cdots\right)\\\\
&\approx \frac{1}{R}-\frac{\varepsilon_{i}}{R^{2}}\\\\
&=\dfrac{R-\varepsilon_{i}}{R^{2}}
\end{align*}
なので,合成抵抗を \( R_{\mathrm{all}}\) とすると,
\begin{align*}
\frac{1}{R_{\mathrm{all}}}&=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\cdots+\frac{1}{R_{N}}\\\\
&\approx\dfrac{R-\varepsilon_{1}}{R^{2}}+\dfrac{R-\varepsilon_{2}}{R^{2}}+\cdots+\dfrac{R-\varepsilon_{N}}{R^{2}}\\\\
&=\frac{NR-\displaystyle \sum_{i=1}^N \varepsilon_{i}}{R^{2}}.
\end{align*}
\frac{1}{R_{\mathrm{all}}}&=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\cdots+\frac{1}{R_{N}}\\\\
&\approx\dfrac{R-\varepsilon_{1}}{R^{2}}+\dfrac{R-\varepsilon_{2}}{R^{2}}+\cdots+\dfrac{R-\varepsilon_{N}}{R^{2}}\\\\
&=\frac{NR-\displaystyle \sum_{i=1}^N \varepsilon_{i}}{R^{2}}.
\end{align*}
よって、
\begin{align*}
R_{\mathrm{all}}&=\frac{R^2}{NR-\displaystyle \sum_{i=1}^N \varepsilon_{i}}\\\\
&=\frac{R^{2}}{NR}\cdot\frac{1}{1-\frac{\scriptsize{\displaystyle \sum_{i=1}^N \varepsilon_{i}}}{NR}}\\\\
&=\frac{R}{N}\left[1+\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{NR}+\left(\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{NR}\right)^{2}+\cdots\right]\\\\
&\approx\frac{R}{N}+\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{N^{2}}
\end{align*}
R_{\mathrm{all}}&=\frac{R^2}{NR-\displaystyle \sum_{i=1}^N \varepsilon_{i}}\\\\
&=\frac{R^{2}}{NR}\cdot\frac{1}{1-\frac{\scriptsize{\displaystyle \sum_{i=1}^N \varepsilon_{i}}}{NR}}\\\\
&=\frac{R}{N}\left[1+\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{NR}+\left(\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{NR}\right)^{2}+\cdots\right]\\\\
&\approx\frac{R}{N}+\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{N^{2}}
\end{align*}
であるから、
\begin{align*}
V(R_{\mathrm{all}})&=V\left(\frac{R}{N}+\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{N^{2}}\right)\\\\
&=\frac{1}{N^4}\left[V(\varepsilon_{1})+V(\varepsilon_{2})\cdots +V(\varepsilon_{N})\right]\\\\
&=\frac{\sigma^{2}}{N^{3}}.
\end{align*}
V(R_{\mathrm{all}})&=V\left(\frac{R}{N}+\frac{\displaystyle \sum_{i=1}^N \varepsilon_{i}}{N^{2}}\right)\\\\
&=\frac{1}{N^4}\left[V(\varepsilon_{1})+V(\varepsilon_{2})\cdots +V(\varepsilon_{N})\right]\\\\
&=\frac{\sigma^{2}}{N^{3}}.
\end{align*}
したがって、 \(N\) 個の抵抗を並列に繋いだ合成抵抗の平均値は \(\frac{R}{N}\) ,標準偏差は \(\frac{\sigma}{N\sqrt{N}}\left(=\frac{\sqrt{N}\sigma}{N^{2}}\right)\) である。
\(N\) 個の抵抗を直列に繋いだ合成抵抗の標準偏差は \( \sqrt{N}\sigma\) だったので、 \(N\) 個の抵抗を並列に繋いだ合成抵抗の標準偏差は直列時の約 \(\frac{1}{N^{2}}\) 倍の大きさになるようです。

コメント