(問題)
$$\int e^{x}\mathrm{sin} x \mathrm{d}x$$ を求めよ
このような問題に対して、高校の教科書では、部分積分の公式
\begin{align*}
\displaystyle\int f'(x)g(x) \mathrm{d}x =f(x)g(x)-\int f(x)g'(x) \mathrm{d}x
\end{align*}
\displaystyle\int f'(x)g(x) \mathrm{d}x =f(x)g(x)-\int f(x)g'(x) \mathrm{d}x
\end{align*}
を用いて解きましょう、ということになっていますが、特に使う必要はありません。
「微分」と「足し算」のみを使って
と計算することができれば、あとは両辺を積分するだけで
\begin{align*}
\displaystyle\int e^x\sin x =\frac{e^x}{2}(\sin x-\cos x)+C
\end{align*}と一瞬で求めることができます
考える順序としては、まず、微分して \(e^{x}\sin x\) が得られる形を考えます。
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}x}(e^x\sin x) =e^x\sin x +e^x\cos x.
\end{align*}
\frac{\mathrm{d}}{\mathrm{d}x}(e^x\sin x) =e^x\sin x +e^x\cos x.
\end{align*}
次に、\(e^x\cos x\) の項を除去できる微分の形を考えます。
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}x}(e^x\cos x) =e^x\cos x -e^x\sin x.
\end{align*}
\frac{\mathrm{d}}{\mathrm{d}x}(e^x\cos x) =e^x\cos x -e^x\sin x.
\end{align*}
あとは、 両式を足して\(e^{x}\mathrm{sin} x\)が得られるよう\(\dfrac{1}{2}\),\(-\dfrac{1}{2}\)といった係数をかけます。最後に両辺を積分すれば解が得られます。
部分積分を覚えていないから解けない、という自体に陥らないようにしておきましょう。
———————————————————————————————
オイラーの公式を知っている方は、部分積分を使わず、次のように求めるのが一般的かもしれません
\begin{align*}
\displaystyle\int e^{x}\mathrm{sin} x \mathrm{d}x &=\displaystyle\int e^{x}\cdot \frac{e^{ix}-e^{-ix}}{2i}\mathrm{d}x\\
&=\frac{1}{2i}\displaystyle\int(e^{(1+i)x}-e^{(1-i)x})\mathrm{d}x\\
&=\frac{1}{2i}\left[\frac{e^{(1+i)x}}{1+i}-\frac{e^{(1-i)x}}{1-i}\right]+C\\
&=\frac{-1-i}{4}e^{(1+i)x}-\frac{-1+i}{4}e^{(1-i)x}+C\\
&=-\frac{1}{2}e^{x}\mathrm{cos} x+\frac{1}{2}e^{x}\mathrm{sin} x+C
\end{align*}
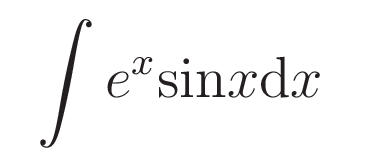
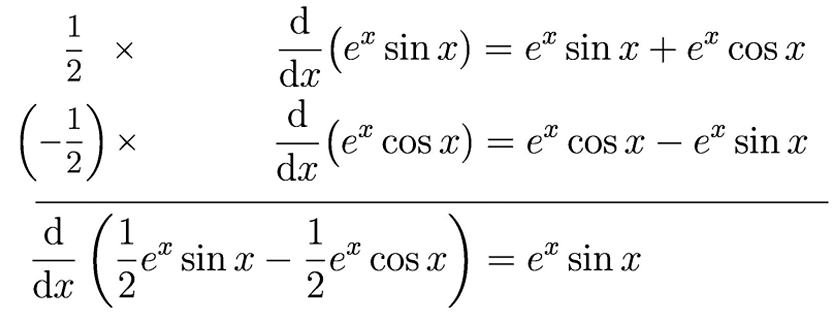
コメント