Excelには双曲線近似の機能はない
Excelには線形近似や対数近似、指数近似など近似曲線を作成してくれる機能がありますが、双曲線近似を作成してくれる機能がありません。では、
\begin{align}
Y=\dfrac{a}{X}
\end{align}
といった近似や
\begin{align}
Y=\dfrac{aX+b}{cX+d}
\end{align}
といった双曲線近似したい場合には、どうしたらいいのか、このページで解説していきたいと思います。
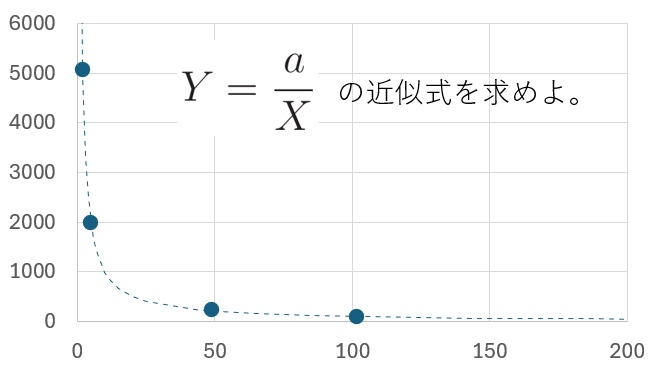
\(y=\frac{a}{X}\) の近似式を作成
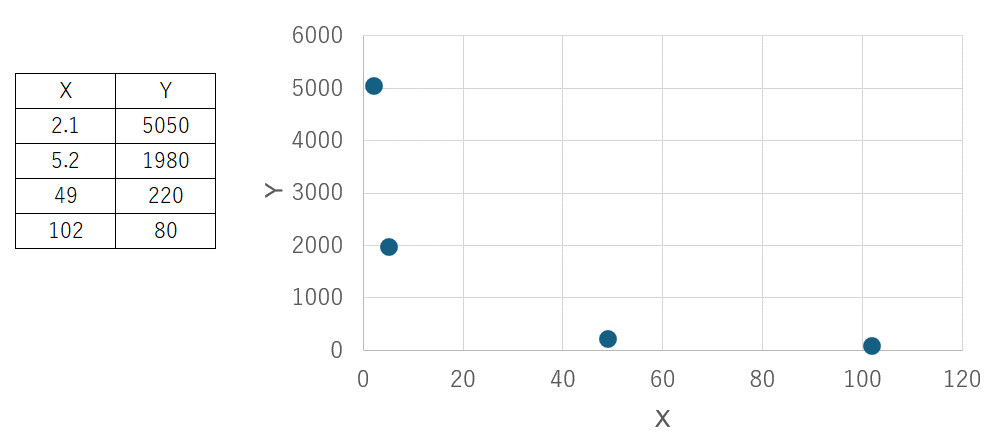
上述の4つのデータから、
\begin{align}
Y=\dfrac{a}{X}
\end{align}
という近似式を求めてみます。
(参考)
上述の4つのデータは \(Y=\dfrac{1000}{X}\)という式をベースにして、\(X\),\(Y\)に誤差を加えたデータになっています。そのため、\(a=1000\) に近しい値の近似式が得られているか確認していきます。
今回、あえて やり方① と やり方② の2つをご紹介しますが、やり方①は非推奨です。やり方①で行ってしまいそうになりますが、やり方②で近似式を作成するようにしましょう。ぜひ結果を比較してみてください。
やり方①
\begin{align}
L(a)=\displaystyle \sum_{i=1}^{4} \left(\frac{a}{X_{i}}-Y_{i}\right)^{2}
\end{align}
を最小とする \(a\) をソルバーで求めます。
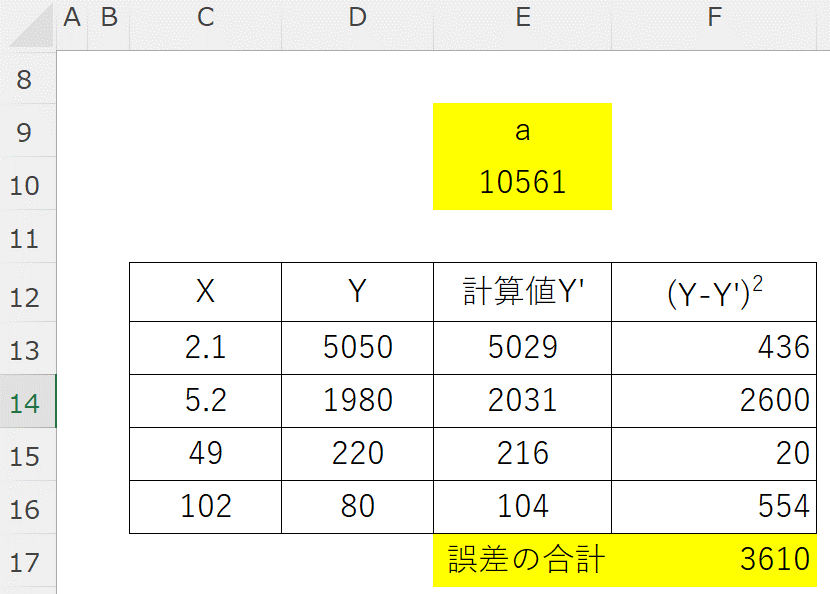
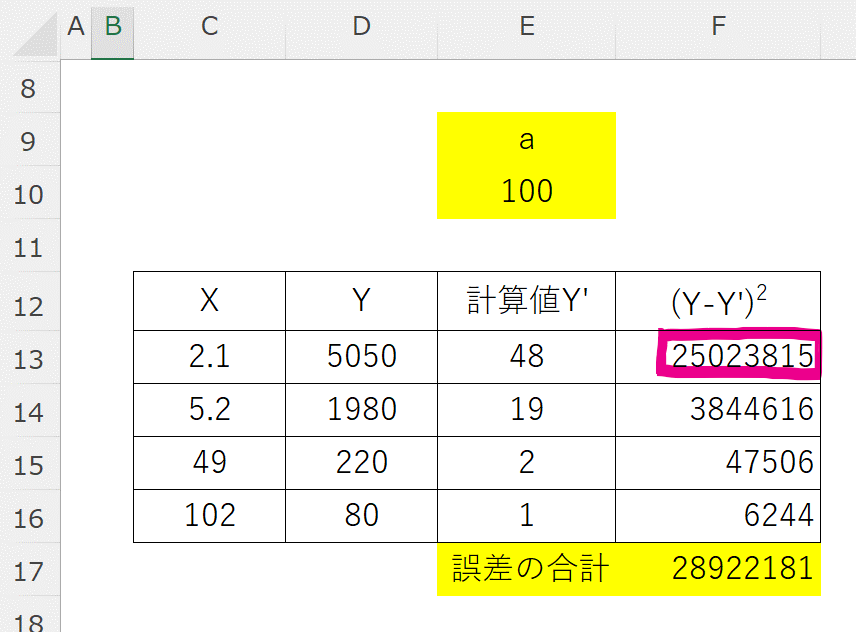
以下のように、\(a\) の初期値は適当に設定(今回は100とした)し、その \(a\) を使って計算した \(Y'(=a/x)\) と \(Y\) との誤差の2乗和 \(\left(Y’_{i}-Y_{i}\right)^{2}\) を計算します。
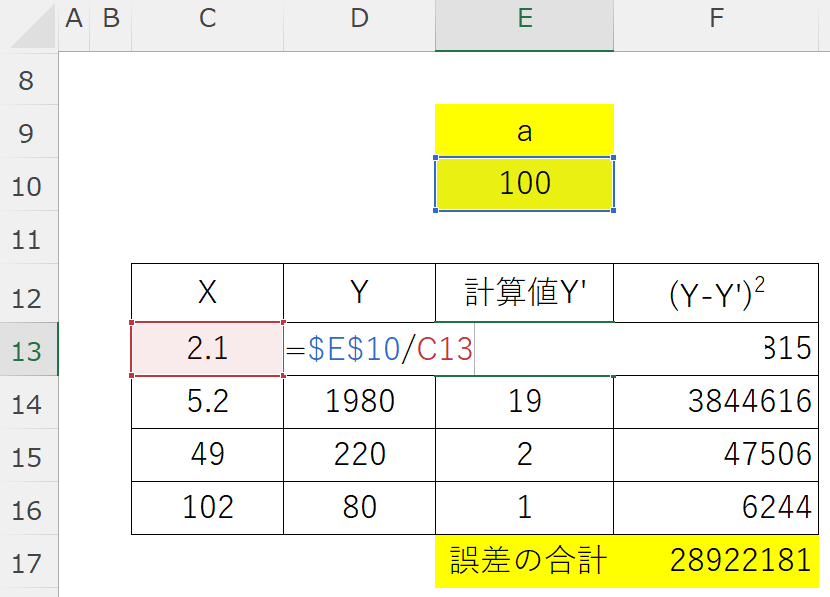
そして、この誤差の2乗和が最小となるような \(a\) を求めるため、ソルバーのパラメーターを以下のように設定して解決ボタンを押します。
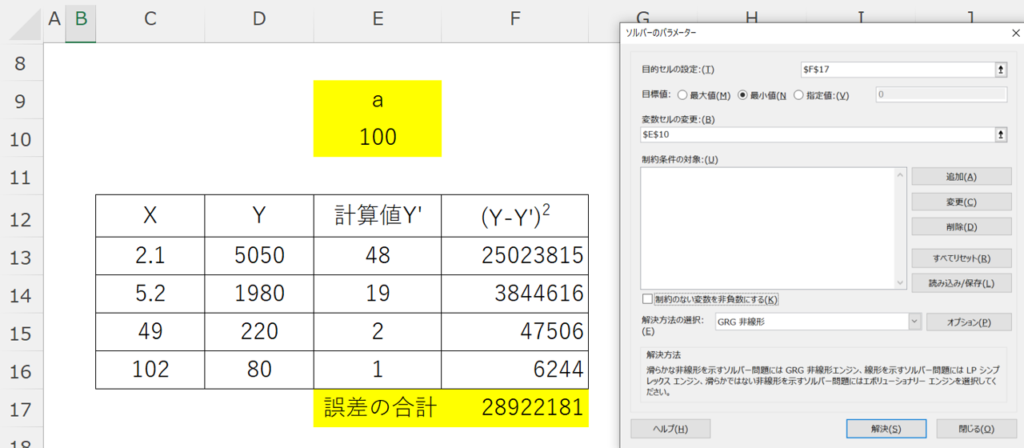
その結果、\(a=10561\) と求められます。
やり方②
\begin{align}
Y_{i}-\dfrac{a}{X{i}}\approx 0
\end{align}
ではなく、
\begin{align}
X_{i}Y_{i}-a \approx 0
\end{align}
であると考え、
\begin{align}
L(a)=\displaystyle \sum_{i=1}^{4} (X_{i}Y_{i}-a)^2
\end{align}
を極小化する \(a\) をソルバーで求めます。
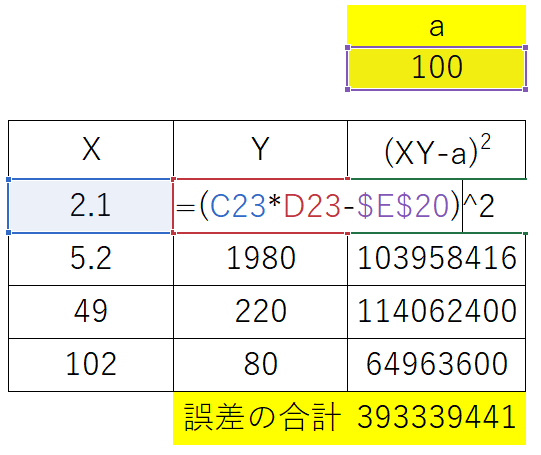
以下のように、\(a\) の初期値は適当に設定(今回は100とした)し、 \( (X_{i}Y_{i}-a)^2\) の和を計算します。
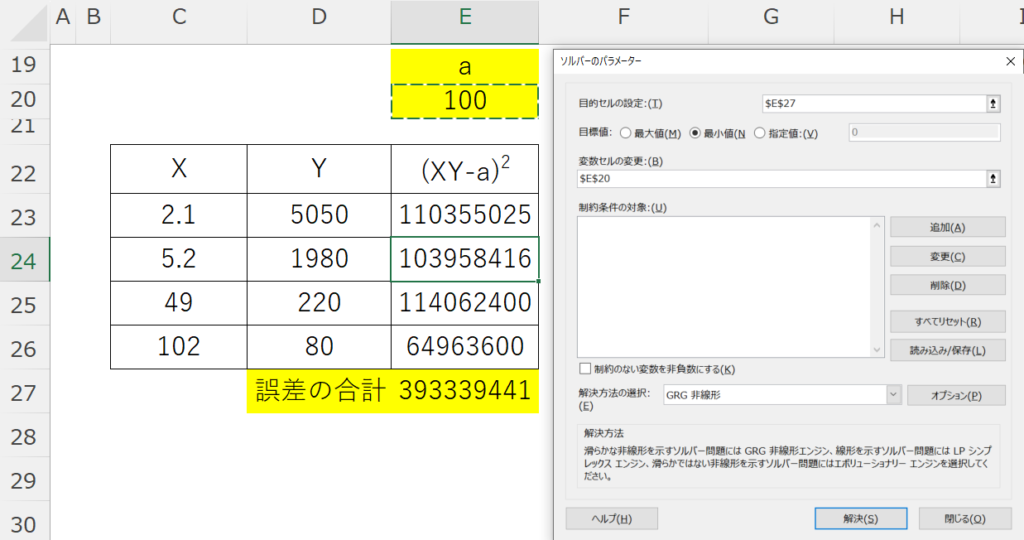
そして、2乗和が最小となるような \(a\) を求めるため、ソルバーのパラメーターを以下のように設定して解決ボタンを押します。
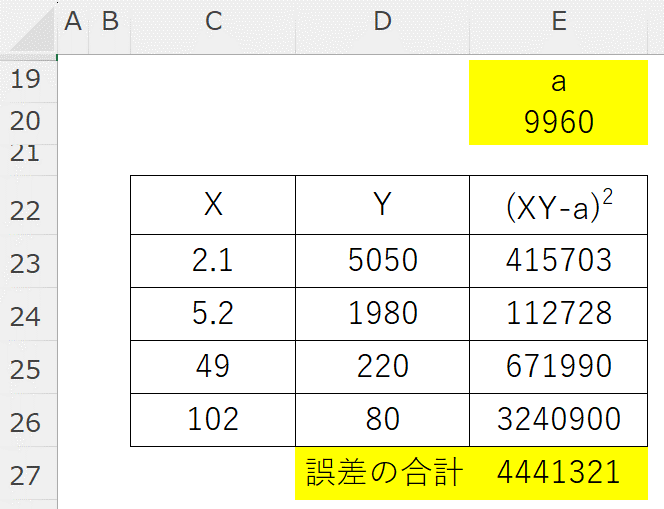
その結果、\(a=9960\) と求められます。
やり方①が非推奨な理由
やり方①:\(a=10561\) 、 やり方①:\(a=9960\) となりました。
\(Y=\dfrac{1000}{X}\) をベースに作成したデータだったので、やり方②の精度が高いことがわかります。
やり方①が非推奨な理由は、\(Y\) の誤差しか考慮していない点にあります。
・\(Y_{1}=5000\) の誤差が+1%だった場合、 \(Y’_{1}=5050\)であり、その誤差の2乗は \(\left(Y_{1}-Y’_{1}\right)^{2}=2500\)
・\(Y_{1}=100\) の誤差が-20%だった場合、 \(Y’_{1}=80\)であり、その誤差の2乗は \(\left(Y_{1}-Y’_{1}\right)^{2}=400\)
となり、誤差の割合としては \(Y_{1}=80\) の方が大きいのに、誤差の2乗の大きさは \(Y_{1}=5050\) の方が大きいため、その誤差を小さくしようと \(Y_{1}=5050\) の方をより重視して \(a\) の値を決めてしまいます。
Excelにおける計算仮定を振り返ると、\(Y\) の値が大きいほど誤差の2乗の値が大きいことがわかります。これでは \(Y\) の値が大きい側のデータに合わせた近似式になってしまいます。
\(Y=\frac{aX+b}{cX+d}\) の近似式を作成
上述の \(Y=\dfrac{a}{X}\) の例で示した「やり方②」と同様の考え方を用います。\begin{align} Y_{i}-\dfrac{aX_{i}+b}{cX_{i}+d}\approx 0 \end{align} ではなく、 \begin{align} Y_{i}(cX_{i}+d)-(aX_{i}+b) \approx 0 \end{align} であると考え、 \begin{align} L(a)=\displaystyle \sum_{i=1}^{n} (Y_{i}(cX_{i}+d)-(aX_{i}+b))^2 \end{align} を極小化する \(a\),\(b\),\(c\),\(d\) をソルバーで求めます。
ただし、 \begin{align} Y=\dfrac{aX+b}{cX+d}=\dfrac{(a/c)X+b/c}{X+d/c} \end{align} であり、自由度は3なので、\(c=1\) とし\(a\),\(b\),\(d\) を変数セルとして設定することが一般的です。

コメント