因数定理を用いて直線の式を求めてみよう

(問題)

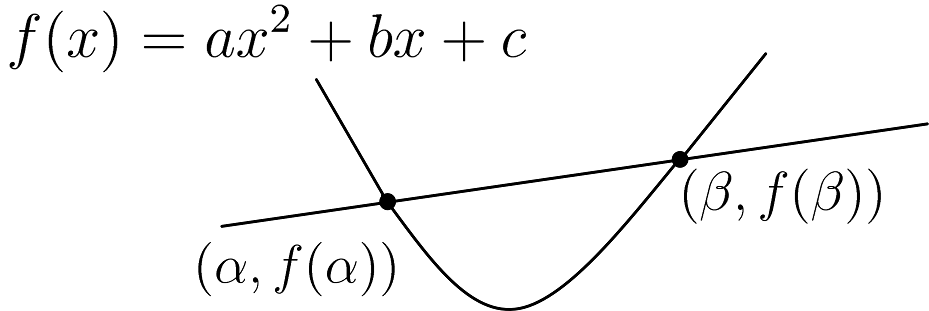
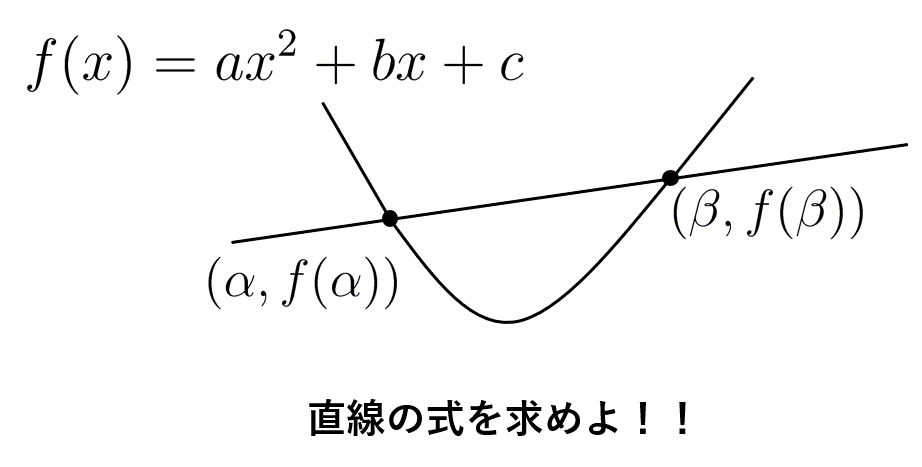
$$f(x)=ax^{2}+bx+c~~~(a\neq0)$$
とするとき，$y=f(x)$ 上の点$ (\alpha,f(\alpha)) $ および$ (\beta,f(\beta)) $ を通る直線の式を求めよ．

直線の方程式を $y=g(x)$ とおくと、

$$f(x)-g(x)=a(x-\alpha)(x-\beta)$$ が成り立つ。

(理由)
$x=\alpha$ において $f(\alpha)=g(\alpha)$ ,　$x=\beta$ において $f(\beta)=g(\beta)$ であるから

\begin{align*} \begin{cases}f(\alpha)-g(\alpha)=0\\f(\beta)-g(\beta)=0\end{cases} \end{align*}
を満たす。つまり、$f(x)-g(x)$ は $(x-\alpha)$ および $(x-\beta)$ を因数に持つ。

よって、 $$g(x)=f(x)-a(x-\alpha)(x-\beta)$$

\begin{align*} g(x)&=f(x)-a(x-\alpha)(x-\beta)\\ &=[b+a(\alpha+\beta)]x+c-a\alpha \beta. \end{align*}