(問題)
\((x^n-1)\) を因数分解せよ。
\((x^n-1)\) を因数分解せよ。
もちろん、答えは
\begin{align*}
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x^{2}+x+1)
\end{align*}
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x^{2}+x+1)
\end{align*}
ですね。
この因数分解を知っていれば、その後、色々役に立つことがあります。
\begin{align*}
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x^{2}+x+1)
\end{align*}
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x^{2}+x+1)
\end{align*}
から、
\begin{align*}
1+x+x^{2}+\cdots+x^{n-2}+x^{n-1}=\frac{x^n-1}{x-1} (x\neq 1).
\end{align*}
1+x+x^{2}+\cdots+x^{n-2}+x^{n-1}=\frac{x^n-1}{x-1} (x\neq 1).
\end{align*}
となります。
ここから、\(|x|\ll 1\) を考えると、
\begin{align*}
\dfrac{1}{1+x}\approx 1-x , \dfrac{1}{1-x}\approx 1+x
\end{align*}
\dfrac{1}{1+x}\approx 1-x , \dfrac{1}{1-x}\approx 1+x
\end{align*}
という高校物理でよく見かける近似式が出てきますね。
また、\(|x|\lt 1\) のとき、指数が最も大きい \(X^{n}=0\) を仮定すると、
\begin{align*}
\dfrac{1}{1+x} &= 1-x+x^{2}-x^{3}+\cdots,\\\\
\dfrac{1}{1-x} &= 1+x+x^{2}+x^{3}+\cdots
\end{align*}
\dfrac{1}{1+x} &= 1-x+x^{2}-x^{3}+\cdots,\\\\
\dfrac{1}{1-x} &= 1+x+x^{2}+x^{3}+\cdots
\end{align*}
というマクローリン展開の式が出てきます。また、この式の両辺を積分すれば
\begin{align*}
\mathrm{log}(1+x) &= x-\dfrac{x^2}{2}+\dfrac{x^3}{2}-\dfrac{x^4}{4}+\cdots,\\\\
\mathrm{log}(1-x) &= x+\dfrac{x^2}{2}+\dfrac{x^3}{2}+\dfrac{x^4}{4}+\cdots
\end{align*}
\mathrm{log}(1+x) &= x-\dfrac{x^2}{2}+\dfrac{x^3}{2}-\dfrac{x^4}{4}+\cdots,\\\\
\mathrm{log}(1-x) &= x+\dfrac{x^2}{2}+\dfrac{x^3}{2}+\dfrac{x^4}{4}+\cdots
\end{align*}
のマクローリン展開も求めることができます。
このように単純な因数分解
\begin{align*}
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x^{2}+x+1)
\end{align*}
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x^{2}+x+1)
\end{align*}
から、色々な情報を紐づけておけば、マクローリン展開など忘れてていても覚えておきやすいですね。


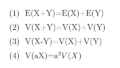
コメント