(問題)
\(A,B,P\) の3点が与えられているとき、\(A,B\) を通過する任意の円に関する \(P\) の極線は定点を通過することを証明せよ。
ただし、定点を通過しない場合もあり、その条件も同時に示せ。 [昭和5年 東京文理大]
\(A,B,P\) の3点が与えられているとき、\(A,B\) を通過する任意の円に関する \(P\) の極線は定点を通過することを証明せよ。
ただし、定点を通過しない場合もあり、その条件も同時に示せ。 [昭和5年 東京文理大]
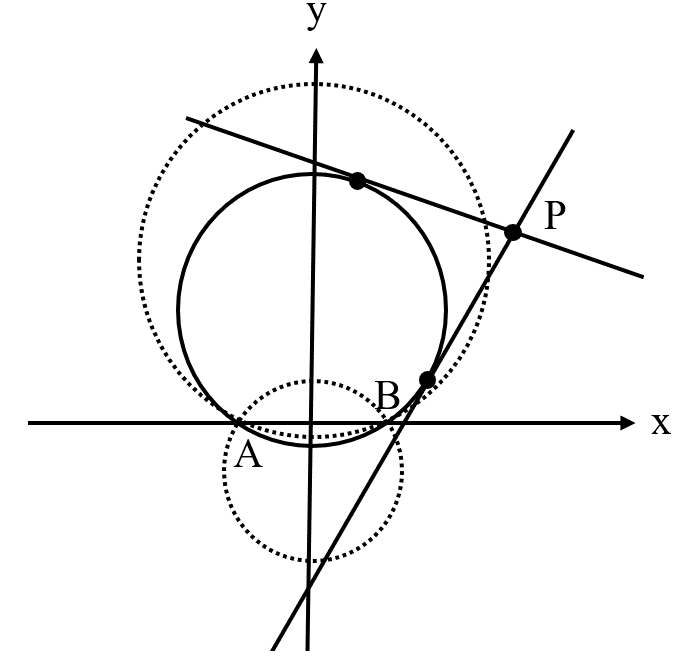
\(A(-a,0)\) , \(B(a,0)\) , \(P(x_{0},y_{0})\) とおくと、\(A,B\) を通過する任意の円は、中心を \((0,h)\) とし、
\begin{align*}
x^{2}+(y-h)^2=a^{2}+h^{2} (a^{2}+h^{2} \lt x^{2}_{0}+(y_{0}-h)^{2})
\end{align*}
x^{2}+(y-h)^2=a^{2}+h^{2} (a^{2}+h^{2} \lt x^{2}_{0}+(y_{0}-h)^{2})
\end{align*}
とおける。\(P\) からこの円に引いた接線の接点の座標を \((X,Y)\) とすると、
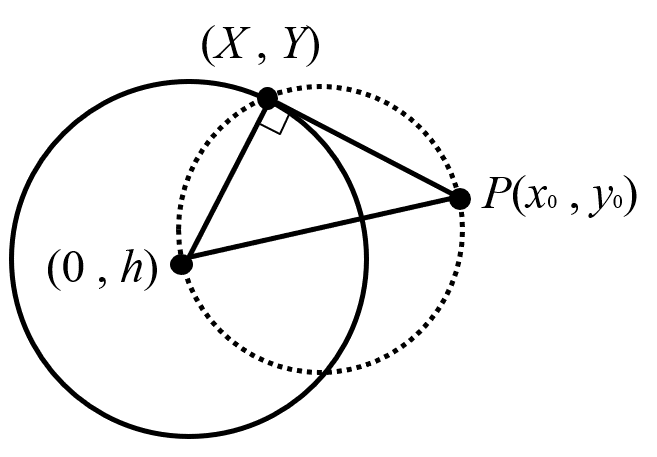
\(X,Y\) が満たすべき方程式は、
\begin{align*}
&\begin{cases}
X^{2}+(Y-h)^{2}=a^{2}+h^{2}\\\\
X(X-x_{0})+(Y-h)(Y-y_{0})=0
\end{cases} \\\\
\Longleftrightarrow&\begin{cases}
X^{2}+(Y-h)^{2}=a^{2}+h^{2}\\\\
x_{0}X+(y_{0}-h)(Y-h)=a^{2}+h^{2}
\end{cases} \\\\
\Longleftrightarrow&\begin{cases}
X^{2}+(Y-h)^{2}=a^{2}+h^{2}\\\\
x_{0}X+(y_{0}-h)Y=y_{0}h+a^{2}.
\end{cases}
\end{align*}
&\begin{cases}
X^{2}+(Y-h)^{2}=a^{2}+h^{2}\\\\
X(X-x_{0})+(Y-h)(Y-y_{0})=0
\end{cases} \\\\
\Longleftrightarrow&\begin{cases}
X^{2}+(Y-h)^{2}=a^{2}+h^{2}\\\\
x_{0}X+(y_{0}-h)(Y-h)=a^{2}+h^{2}
\end{cases} \\\\
\Longleftrightarrow&\begin{cases}
X^{2}+(Y-h)^{2}=a^{2}+h^{2}\\\\
x_{0}X+(y_{0}-h)Y=y_{0}h+a^{2}.
\end{cases}
\end{align*}
よって、極線の方程式は、
\begin{align*}
x_{0}x+(y_{0}-h)y=y_{0}h+a^{2}.
\end{align*}
x_{0}x+(y_{0}-h)y=y_{0}h+a^{2}.
\end{align*}
\(x_{0}=0\)、すなわち、\(P\) が \(AB\) の垂直二等分線上にあるとき、
\begin{align*}
&x_{0}x+(y_{0}-h)y=y_{0}h+a^{2}\\\\
\Longleftrightarrow &(y_{0}-h)y=y_{0}h+a^{2}
\end{align*}
&x_{0}x+(y_{0}-h)y=y_{0}h+a^{2}\\\\
\Longleftrightarrow &(y_{0}-h)y=y_{0}h+a^{2}
\end{align*}
となり、定点を通る直線群とはならない.
\(x_{0}\neq 0\)、すなわち、\(P\) が \(AB\) の垂直二等分線上にないとき、
\begin{align*}
&x_{0}x+(y_{0}-h)y=y_{0}h+a^{2}\\\\
\Longleftrightarrow &x_{0}\left(x-\frac{y_{0}^{2}+a^{2}}{x_{0}}\right)+(y_{0}-h)(y+y_{0})=0
\end{align*}
&x_{0}x+(y_{0}-h)y=y_{0}h+a^{2}\\\\
\Longleftrightarrow &x_{0}\left(x-\frac{y_{0}^{2}+a^{2}}{x_{0}}\right)+(y_{0}-h)(y+y_{0})=0
\end{align*}
となり、この直線は \(h\) の値によらず、定点\(\left(\frac{y_{0}^{2}+a^{2}}{x_{0}},-y_{0}\right)\)を通る.(証明終)
問題の解答は以上ですが、一般的な極線の方程式の求め方を振り返っておきましょう。
円 \((x-a)^{2}+(y-b)^{2}=r^{2}\) の外部の点P\((x_{0},y_{0})\) からこの円に引いた接線の接点の座標を \(X,Y)\) とおくと、\(X,Y\) が満たすべき方程式は、
\begin{align*}
&\begin{cases}
(X-a)^{2}+(Y-b)^{2}=r^{2}\\\\
(X-a)(X-x_{0})+(Y-b)(Y-y_{0})=0
\end{cases} \\\\
\Longleftrightarrow & \begin{cases}
(X-a)^{2}+(Y-b)^{2}=r^{2}\\\\
(x_{0}-a)(X-a)+(y_{0}-b)(Y-b)=r^{2}.
\end{cases}
\end{align*}
&\begin{cases}
(X-a)^{2}+(Y-b)^{2}=r^{2}\\\\
(X-a)(X-x_{0})+(Y-b)(Y-y_{0})=0
\end{cases} \\\\
\Longleftrightarrow & \begin{cases}
(X-a)^{2}+(Y-b)^{2}=r^{2}\\\\
(x_{0}-a)(X-a)+(y_{0}-b)(Y-b)=r^{2}.
\end{cases}
\end{align*}
このように、接点の方程式と円の式から、極線の方程式 \((x_{0}-a)(X-a)+(y_{0}-b)(Y-b)=r^{2}\) を求めることができます。


コメント